Complétez la grille ci-après à l'aide des définitions suivantes.

1. Adjectif attribué à une famille de vecteurs \((u_1,u_2,\cdots,u_p)\) de \(E\) telle que \(E=\text{Vect}(u_1,u_2,\cdots,u_p)\).
2. Nom donné à une famille libre et génératrice de \(E\).
3. Nom donné à l'ensemble \(\big\{u\in E,\ f(u)=0_F\big\}\) lorsque \(f\) est une application linéaire de \(E\) dans \(F\).
4. Adjectif caractérisant une application \(f:E\rightarrow F\) telle que:
   \(\forall \lambda\in \mathbb{K},\ \forall (u,v)\in E^2, \ f(\lambda u +v)=\lambda f(u)+f(v).\)
5. Adjectif caractérisant une application linéaire \(f\in\mathscr{L}(E,F)\) telle que \(\text{Ker}(f)=\big\{0_E\big\}\).
6. La matrice \(\begin{pmatrix}\lambda_1\\\vdots\\\lambda_n\end{pmatrix}\) représente les \(\cdots?\cdots\) du vecteur \(u=\lambda_1u_1+\cdots+\lambda_n u_n\) dans la base \(\mathscr{B}=(u_1,u_2,\cdots,u_n)\) de \(E\).
7. Nom donné à la dimension de \(\text{Im}(f)\).
8. Adjectif donné à un sous-espace vectoriel \(F\) pour lequel il existe des vecteurs \(u_1,\ u_2, \cdots, u_p\) tels que \(F=\text{Vect}(u_1,u_2,\cdots,u_p)\).
9. Cardinal d'une base.
10. Adjectif caractérisant une application linéaire \(f\in\mathscr{L}(E,F)\) telle que \(\text{rg}(f)=\dim(F)\).
11. Adjectif caractérisant une famille de vecteurs \((u_1,u_2,\cdots,u_p)\) telle que \(\text{rang}(u_1,u_2,\cdots,u_p)=p\).
12. Nom donné à l'ensemble \(\big\{f(u),\ u\in E\big\}\).

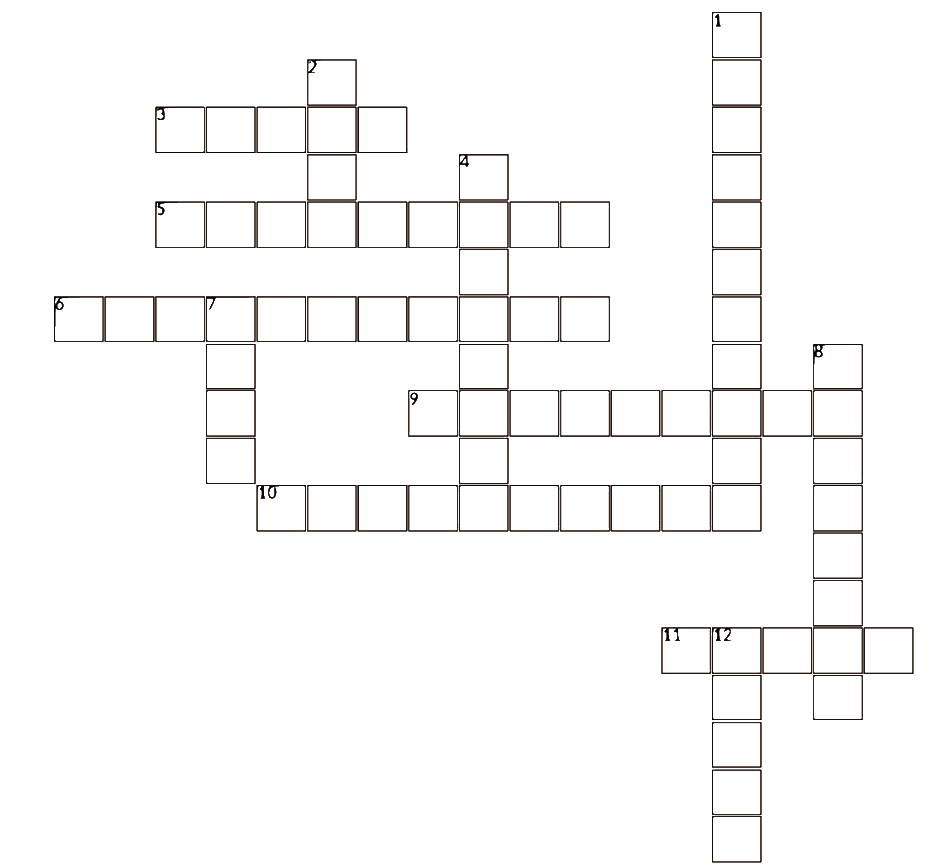
Vous pensez avoir trouvé toutes les bonnes réponses ? Inscrivez le mot formé par les cases 2, 5, 7, 8 et 11.