Satanée souris
Cher amateur de Sudoku,
Je pense avoir trop mangé hier et te prie de bien vouloir m'excuser pour les dégâts occasionnés sur ta grille. Je t'ai noté ci-dessous les valeurs des cases manquantes.
la souris.
\[ \begin{array}{ll} \displaystyle \textnormal{F8 : } \sum_{n=0}^\infty \frac{2^n}{3^n} & \displaystyle\textnormal{B5 : } 2\sum_{n=0}^\infty \frac{n}{2^n} \\ \displaystyle\textnormal{H5 : } \sum_{n=1}^\infty \frac{1}{n(n+1)}\quad~ & \displaystyle\textnormal{I2 : } \ln\left(\sum_{n=0}^\infty \frac{7^n}{n!}\right) \end{array} \]
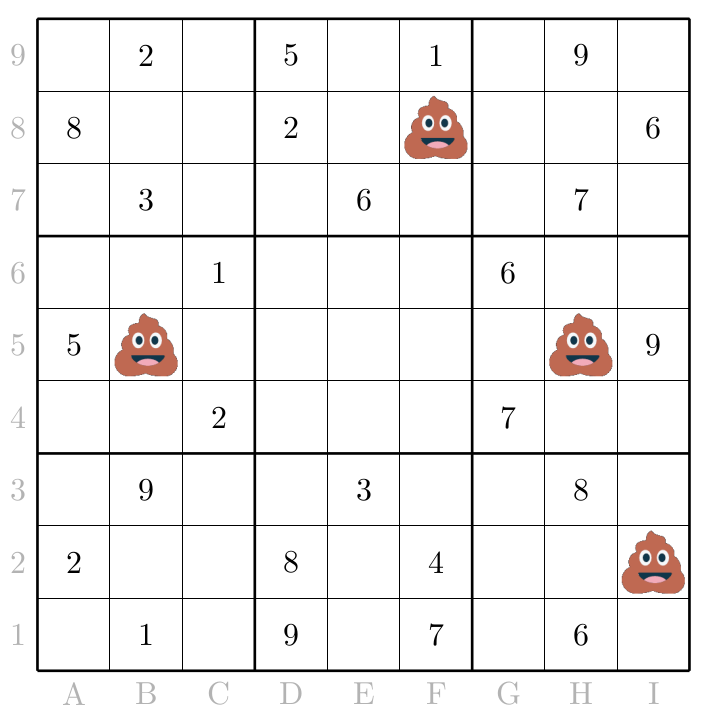
Ps : je t'ai laissé un cadeau, tu le trouveras en rentrant les valeurs des cases D5, E5 et F5 séparées par des tirets.

