La suite de l'épopée du lutin
Hier, pour pouvoir s'installer dans son nid douillet, notre lutin a délogé
les 3 oeufs qui y étaient lotis, en les lançant dans le vide.
Ils sont tombés sur le carré magique que le Père-Noël s'apprêtait à résoudre sous le sapin en attendant le retour du lutin.
Aidez le Père Noël à enlever les oeufs de la grille puis à compléter son carré magique !
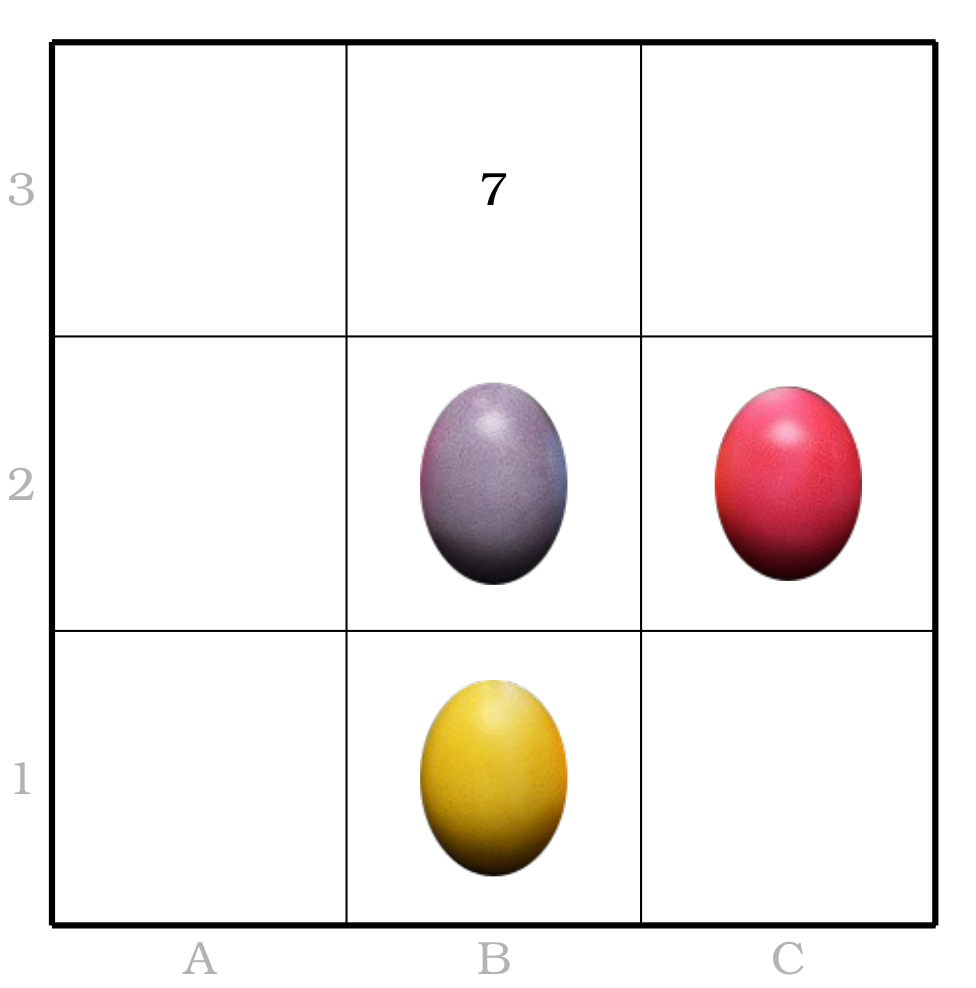 On considère l'application bijective
\[ \begin{array}{ccccc}
f & \colon & \left[\!\left[0,4\right]\!\right] & \rightarrow & \left[\!\left[1,5\right]\!\right] \\
& &0 & \mapsto & 4 \\
&&1 & \mapsto & 2 \\
&&2 & \mapsto & 5 \\
&&3 & \mapsto & 1 \\
&&4 & \mapsto & 3
\end{array}\]
et l'application
\[\begin{array}{ccccc}
g & \colon & \big\{\square,\triangle\big\} & \rightarrow & \big\{1;2\big\} \\
&&\square & \mapsto & 1 \\
&&\triangle & \mapsto & 2.
\end{array}\]
On note \(f^{-1}\) la bijection réciproque de \(f\).
On considère l'application bijective
\[ \begin{array}{ccccc}
f & \colon & \left[\!\left[0,4\right]\!\right] & \rightarrow & \left[\!\left[1,5\right]\!\right] \\
& &0 & \mapsto & 4 \\
&&1 & \mapsto & 2 \\
&&2 & \mapsto & 5 \\
&&3 & \mapsto & 1 \\
&&4 & \mapsto & 3
\end{array}\]
et l'application
\[\begin{array}{ccccc}
g & \colon & \big\{\square,\triangle\big\} & \rightarrow & \big\{1;2\big\} \\
&&\square & \mapsto & 1 \\
&&\triangle & \mapsto & 2.
\end{array}\]
On note \(f^{-1}\) la bijection réciproque de \(f\).
 On considère l'application bijective
\[ \begin{array}{ccccc}
f & \colon & \left[\!\left[0,4\right]\!\right] & \rightarrow & \left[\!\left[1,5\right]\!\right] \\
& &0 & \mapsto & 4 \\
&&1 & \mapsto & 2 \\
&&2 & \mapsto & 5 \\
&&3 & \mapsto & 1 \\
&&4 & \mapsto & 3
\end{array}\]
et l'application
\[\begin{array}{ccccc}
g & \colon & \big\{\square,\triangle\big\} & \rightarrow & \big\{1;2\big\} \\
&&\square & \mapsto & 1 \\
&&\triangle & \mapsto & 2.
\end{array}\]
On note \(f^{-1}\) la bijection réciproque de \(f\).
On considère l'application bijective
\[ \begin{array}{ccccc}
f & \colon & \left[\!\left[0,4\right]\!\right] & \rightarrow & \left[\!\left[1,5\right]\!\right] \\
& &0 & \mapsto & 4 \\
&&1 & \mapsto & 2 \\
&&2 & \mapsto & 5 \\
&&3 & \mapsto & 1 \\
&&4 & \mapsto & 3
\end{array}\]
et l'application
\[\begin{array}{ccccc}
g & \colon & \big\{\square,\triangle\big\} & \rightarrow & \big\{1;2\big\} \\
&&\square & \mapsto & 1 \\
&&\triangle & \mapsto & 2.
\end{array}\]
On note \(f^{-1}\) la bijection réciproque de \(f\).
-
 = \(\displaystyle \left(f\circ g\right)(\triangle)\)
= \(\displaystyle \left(f\circ g\right)(\triangle)\)
-
 = \(\displaystyle f^{-1}(1)\)
= \(\displaystyle f^{-1}(1)\)
-
 = \(\displaystyle \left(f^{-1}\circ f^{-1}\right)(5)\)
= \(\displaystyle \left(f^{-1}\circ f^{-1}\right)(5)\)

