Complétez la grille pour retrouver le porte-avions (5 cases)! Chacune des affirmations ci-dessous est vraie si et seulement si le porte-avions se trouve sur la case correspondante. Attention, deux bateaux ne peuvent pas se toucher...

• A3 : Un système linéaire de \(3\) équations à \(5\) inconnues admet une infinité de solutions.
• I5 : Si \(A\) et \(B\) sont deux matrices de même ordre, alors \( ^t(A+B) = {}^tA + {}^tB \).
• D1 : Si \(A \in M_{3,2}(\mathbb{R})\) et \(B \in M_{3,2}(\mathbb{R})\), alors \(AB \in M_{3,2}(\mathbb{R})\).
• J5 : Si une matrice \(A\) vérifie \(A^2 = A\), alors elle est inversible.
• I2 : La matrice \(A = \begin{pmatrix}-1 & 0 & 2 \\ 0 & 4 & 3 \\ 1 & 1 & 1\end{pmatrix}\) est inversible.
• I6 : La matrice \(\begin{pmatrix}7 & 1 & 2 \\ 5 & 3 & 1 \\ 4 & 5 & 7\end{pmatrix}\) est symétrique.
• G8 : Si \(N \in \mathbb{N}\) et \((A,B) \in (M_n(\mathbb{R}))^2\) avec \(n \in \mathbb{N}^*\), alors \[(A+B)^N = \sum_{k=0}^N \binom{N}{k} A^k B^{N-k}\].

Complétez alors la grille:

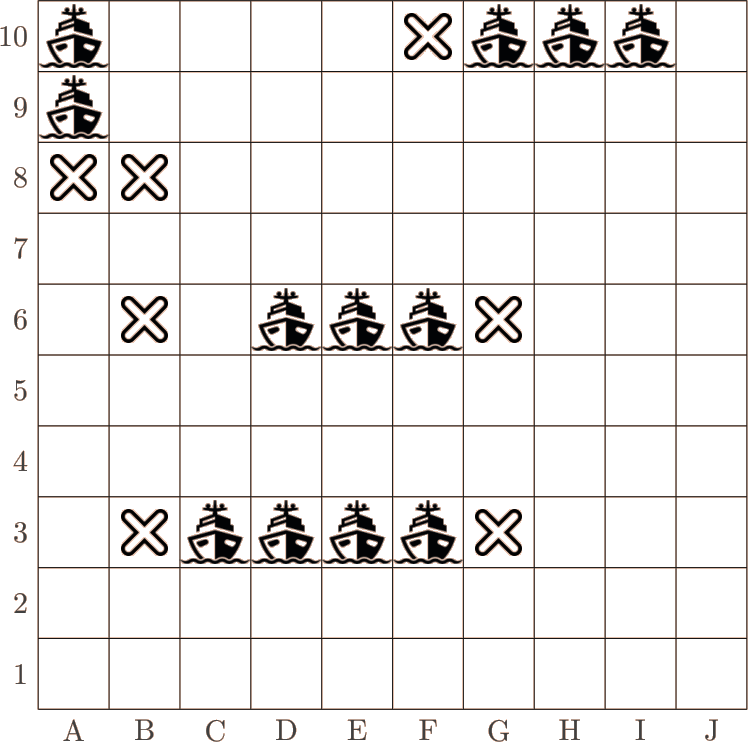
Entrez ci-dessous les coordonnées des extrêmités (par ordre alphabétique/croissant) du porte-avion, séparées par un tiret. Par exemple, si le porte-avion est sur les cases A1, A2, A3, A4 et A5, vous devrez entrer A1-A5.