Cher Monsieur le Détective Privé,

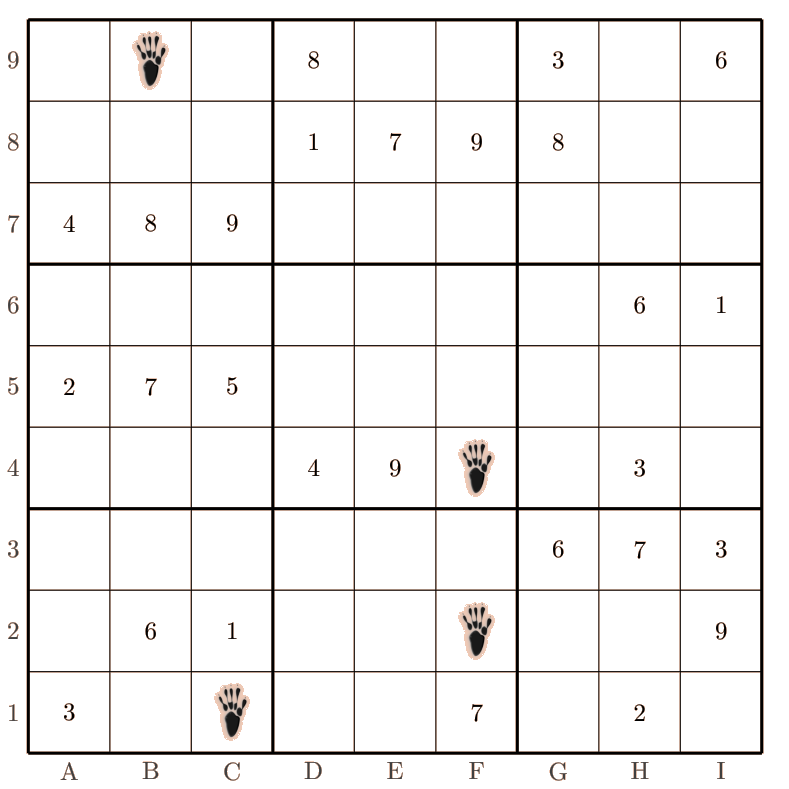
Je fais appel à vos services pour déterminer quel individu a sauvagement piétiné mon Sudoku. Je compte sur vous pour résoudre cette enquête dans les plus brefs délais.

Madame M

Après avoir relevé les empreintes de pas, le détective procède au nettoyage de la scène de crime. Aidez-le afin de pouvoir retrouver les chiffres inscrits dans les cases piétinées.

• En B9 : \( a_2 \) tel que \( \displaystyle\frac{\mathrm{e}^{2x}}{1+3x} = a_0 + a_1x + a_2x^2 + x^2\varepsilon(x) \), où \( \varepsilon(x) \underset{x\to0}{\rightarrow} 0 \)
• En F4 : \( a_0 \) tel que \( \sqrt{x} = a_0 + a_1(x-4) + (x-4)\varepsilon(x) \), où \( \varepsilon(x) \underset{x\to4}{\rightarrow} 0 \)
• En F2 : \( f''(0) \) où \( f : x \mapsto x - 4\sqrt{1-x}\cos(x) \) à calculer sans dériver \( f \)...
• En C1 : \( a_1 \) tel que \( (x+2)^2 = a_0 + a_1 x + x\varepsilon(x) \), où \( \varepsilon(x) \underset{x\to0}{\rightarrow} 0 \)

Pour connaître l'identité du coupable, entrez D5-E5-F5 où D5, E5 et F5 sont à remplacer par les chiffres que vous avez trouvés dans les cases D5, E5 et F5.